Matemática -
Vejamos por meio de um problema hipotético, como a matemática pode nos ajudar a programar uma dieta ao menor custo possível.
Sabendo que uma pessoa em dieta deve ingerir , no máximo, 20 unidades de calorias e 10 de gordura e, no mínimo, 2 unidades de vitamina, qual a melhor programação de compra dos alimentos X e Y de tal forma que a pessoa possa cumprir sua dieta ao menor custo possível sendo fornecidos os dados abaixo?
| Alimento | Caloria | Gordura | Vitamina | Preço por unidade |
| X | 4 | 1 | 1 | R$ 3 |
| Y | 1 | 2 | - | R$ 2 |
Vejamos inicialmente uma combinação possível de quantidades de alimentos X e Y que atendem às restrições de caloria, gordura e vitamina.
Uma alocação poderia ser a compra de duas unidades do alimento X e duas do alimento Y. Nesse caso, a pessoa não estaria ultrapassando o limite de calorias e gordura, além de estar ingerindo vitaminas dentro do limite mínimo necessário (10, 6 e 2 unidades, respectivamente). Sabemos que o gasto total nessa compra seria de R$ 10, mas não temos garantia de que a combinação escolhida de X e de Y seja a que produz o menor gasto possível.
Para encontrarmos a solução ótima do problema devemos inicialmente equacionar as restrições e, em seguida, representá-las no plano cartesiano.
Chamando de x a quantidade comprada do alimento X e de y a quantidade do alimento Y, a restrição de consumo máximo de 20 unidades de caloria pode ser expressa como 4x + y <= 20 (reflita sobre esse resultado!).
De forma análoga, podemos expressar a restrição de consumo máximo de gordura por x + 2y <= 10 e a restrição de limite mínimo de vitaminar por x >= 2.
A representação gráfica da região que atende às três restrições do problema ao mesmo tempo é a região poligonal pintada na figura.
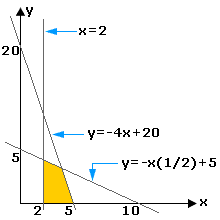 | |
Se houver uma única solução ótima para um problema como esse, pode-se demonstrar que ele será dada por uma dos vértices da poligonal das restrições, no caso do problema por (2,12), (2,0), (5,)) ou (30/7, 20/7). Como o preço unitário de x é R$ 3 e o de y R$ 2, basta verificar qual dos pares (x,y) minimiza o gasto total 3x + 2y. Fazendo as contas, concluímos que a compra ideal é a de duas unidades de x e zero de y totalizando uma gasto mínimo igual a R$ 6. *José Luiz Pastore Mello é mestre em ensino de matemática pela USP e professor do Colégio Santa Cruz
ID: {{comments.info.id}}
URL: {{comments.info.url}}
Ocorreu um erro ao carregar os comentários.
Por favor, tente novamente mais tarde.
{{comments.total}} Comentário
{{comments.total}} Comentários
Seja o primeiro a comentar
Essa discussão está encerrada
Não é possivel enviar novos comentários.
Essa área é exclusiva para você, assinante, ler e comentar.
Só assinantes do UOL podem comentar
Ainda não é assinante? Assine já.
Se você já é assinante do UOL, faça seu login.
O autor da mensagem, e não o UOL, é o responsável pelo comentário. Reserve um tempo para ler as Regras de Uso para comentários.