Matemática -
Existe alguma relação entre uma simples bola de futebol, a química, a geometria e algumas técnicas de contagem?
Vejamos!
Em 1985, foi descoberta uma nova forma de carbono, chamada BUCKMINSTERFULLERENE ou "BUCKYBALL". É a mais estável de uma família de moléculas de carbono conhecida como Fulerenes.
Como o próprio nome sugere, "BUCKYBALL" possui a forma geométrica de uma bola de futebol.
Ao ser observada mais atentamente, constata-se que a molécula é formada por 20 hexágonos e 12 pentágonos, com átomos de carbono localizados nos vértices e ligações químicas representando as arestas.
e matemática do "Buckyball"
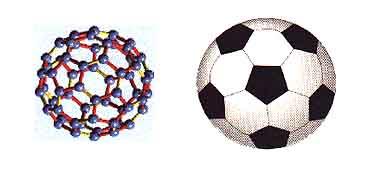
modelo químico modelo matemático
Surgem então algumas questões de caráter matemático:
1) Quantas arestas existem no "Buckyball"?
2) Quantos vértices existem no "Buckyball"?
Vamos estabelecer processos de contagem a fim de responder as questões acima
DE ARESTAS |
Inicialmente vamos representar o número de arestas pela letra A.
O esquema a seguir representa um "pedaço" da molécula devidamente planificado.
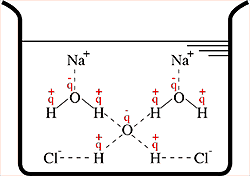
Temos na molécula 20 hexágonos e como cada hexágono possui 6 lados (arestas na molécula), obtém-se:
20.6 = 120 arestas provenientes dos hexágonos.
Temos também 12 pentágonos e como cada pentágono contribui com 5 lados (arestas na molécula), obtém-se:
12.5 = 60 arestas provenientes dos pentágonos
Agora, observando o esquema acima, note que ao contarmos as arestas pertencentes ao hexágono H e as arestas pertencentes ao pentágono P, contamos a aresta AB duas vezes.
Assim sendo, no final do processo de contagem, todas as arestas foram contadas duas vezes, logo, o número correto de arestas é expresso por:
![]()
DE VÉRTICES |
Inicialmente vamos representar o número de vértices pela letra V.
Contaremos o número de vértices através do número de arestas. Observando o esquema anterior nota-se que em cada vértice "chegam" 3 arestas, logo é natural imaginarmos que o número de arestas é o triplo do número de vértices, ou seja, A = 3.V.
Entretanto, ao contarmos as arestas que "chegam" no vértice A e no vértice B (veja esquema acima), contamos a aresta AB duas vezes.
Assim, no final do processo de contagem, todas as arestas foram contadas duas vezes e o número correto de arestas fica então dado por
A = 3 . V
2
O que, isolando o V, nos leva à
V = 2 . A
3
Como A = 90, concluímos que
V =2 . 90 = 60
3
É pelo fato de conter 60 vértices na sua estrutura geométrica (na verdade 60 átomos de carbono) que a fórmula molecular do "Buckyball" é representada por C60.
O modelo químico apresentado pertence a uma família de objetos matemáticos denominada Poliedros Convexos.
No século XVIII, Leonhard Euler, matemático de origem Suíça, encontrou uma relação algébrica que associa o número de arestas A de um poliedro convexo fechado ("sem buracos"), com o número de vértices V e o número de faces F, expressa por:
Esta é a nossa dica da vez.
Não esqueça.
Em todo poliedro convexo fechado vale a relação de Euler:
Teste seus conhecimentos
- 1.(PUC-SP) O número de vértices de um poliedro convexo que possui 12 faces triangulares é:
a) 4
b) 12
c) 10
d) 6
e) 8
- 2.(Cesgranrio-RJ) Um poliedro convexo é formado por 80 faces triangulares e 12 pentagonais. O número de vértices do poliedro é:
a) 80
b) 60
c) 50
d) 48
e) 36
- 3.(PUCCAMP-SP) O "cubo octaedro" é um poliedro que possui 6 faces quadrangulares e 8 triangulares. O número de vértices desse poliedro é:
a) 12
b) 16
c) 10
d) 14
e) n.d.a.
GABARITO: 01) e 02) b 03) a
ID: {{comments.info.id}}
URL: {{comments.info.url}}
Ocorreu um erro ao carregar os comentários.
Por favor, tente novamente mais tarde.
{{comments.total}} Comentário
{{comments.total}} Comentários
Seja o primeiro a comentar
Essa discussão está encerrada
Não é possivel enviar novos comentários.
Essa área é exclusiva para você, assinante, ler e comentar.
Só assinantes do UOL podem comentar
Ainda não é assinante? Assine já.
Se você já é assinante do UOL, faça seu login.
O autor da mensagem, e não o UOL, é o responsável pelo comentário. Reserve um tempo para ler as Regras de Uso para comentários.