Matemática -

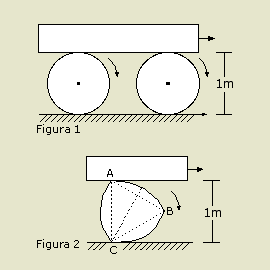
Um mecanismo muito conhecido desde os tempos antigos para transportar blocos de pedra consiste em apoiar o bloco sobre cilindros rolantes.

Esse método, usado até mesmo pelos antigos egípcios no deslocamento de monolitos durante a construção das pirâmides, apóia-se no fato de que o diâmetro constante de uma circunferência garante o transporte do bloco da forma menos irregular possível já que ele sempre estará a uma distância fixa do chão. A pergunta que proponho é a seguinte: será que existe alguma outra figura, além da circunferência, que, ao rolar, também garanta a distância fixa do bloco ao solo?

Por mais estranho que possa parecer, existem muitas figuras com tal propriedade, e uma delas é conhecida como triângulo de Reuleaux, em homenagem ao engenheiro alemão que foi o primeiro a registrar suas propriedades no século passado.

Apesar do nome, um triângulo de Reuleaux não é propriamente um triângulo, mas, sim, uma curva que pode ser formada a partir de um triângulo equilátero ABC: partindo de um triângulo equilátero ABC de lado 1 m, faça três arcos de circunferência de raio 1 m centrados em A, B e C respectivamente e você terá um triângulo de Reuleaux.

É curioso notar que existem muitas outras curvas de largura constante, como o triângulo de Reuleaux ou a circunferência, formadas a partir de polígonos regulares com um número ímpar de lados. Curvas como essas são usadas, por exemplo, nas moedas britânicas de 20 e de 50 pence, cuja forma se aproxima da de um heptágono regular, uma vez que as máquinas de refrigerantes ou jogos são concebidas para aceitar apenas moedas de diâmetro bem determinado.

Outra fabulosa aplicação do triângulo de Reuleaux se deve ao engenheiro inglês Harry James Watt, que, em 1914, aproveitando as propriedades da curva, concebeu uma broca de furadeira com eixo flexível para fazer furos na forma aproximada de um quadrado. *José Luiz Pastore Mello é mestre em ensino de matemática pela USP e professor do Colégio Santa Cruz