Unicamp 2008 - 2^a fase
As retas de equações y = ax + b e y = cx são ilustradas na figura abaixo. Sabendo que o coeficiente b é igual à média aritmética dos coeficientes a e c.

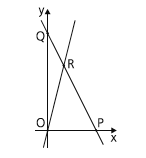a) expresse as coordenadas dos pontos P, Q e R em termos dos coeficientes a e b.
b) determine a, b e c sabendo que a área do triângulo POR é o dobro da área do triângulo ORQ e que o triângulo OPQ tem área 1.

Unicamp 2007 - 2^a fase
Seja dada a reta x - 3y + 6 = 0 no plano xy.

a) Se P é um ponto qualquer desse plano, quantas retas do plano passam por P e formam um ângulo de 45^o com a reta dada acima?
b) Para o ponto P com coordenadas (2,5), determine as equações das retas mencionadas no item (a).

Fuvest 2007 - 2^a fase
Na figura ao lado, os pontos A₁, A₂, A₃, A₄, A₅, A₆ são vértices de um hexágono regular de lado 3 com centro na origem O de um sistema de coordenadas no plano. Os vértices A₁ e A₄ pertencem ao eixo x. São dados também os pontos B = (2,0) e C = (0,1).

Considere a reta que passa pela origem O e intersecta o segmento no ponto P, de modo que os triângulos OPB e OPC tenham a mesma área. Nessas condições, determine

a) a equação da reta .
b) os pontos de intersecção da reta com o hexágono.

FGV 2009 - 2^a fase
No plano cartesiano, são dadas as retas r de equação , e s de equação y = x + 7. Se θ é a medida, em graus, do maior ângulo do triângulo formado pelas retas r, s e o eixo x, determine:

a) o valor do ângulo θ.
b) a área desse triângulo.

FGV 2007 - 2^a fase
Determine a área da região limitada pelas curvas: