Guia de estudos: confira 10 temas essenciais de matemática

Ter domínio de conceitos como porcentagem, funções trigonométricas e probabilidade auxilia na hora de realizar uma boa prova de matemática nos principais vestibulares do país. O UOL consultou professores sobre os dez conteúdos da disciplina que mais caem nos exames.

Esse é o segundo roteiro de uma série que trará o guia de estudos de uma disciplina por dia. Confira o roteiro de química. 

Para José Augusto, professor do colégio Magnum Cidade Nova, em Belo Horizonte, o perfil das questões de matemática vem mudando com o passar do tempo. No Enem, por exemplo, há muita cobrança de interpretação de gráficos, tabelas e variação de grandezas -- tendência seguida por outras provas. “É uma prova relativamente fácil, por isso as médias da disciplina estão subindo”, analisa.

Confira a seguir, um compilado com dez temas importantes mencionados pelos professores dos cursinhos CPV, Nelio Kikuchi, e Oficina do Estudante, Rodolfo Pereira Borges.

• Problemas que envolvem cálculo de porcentagem

Assunto bastante cobrado nos vestibulares, geralmente contextualizado em questões que envolvem o cotidiano ou em matemática financeira. O professor Rodolfo, da Oficina do Estudante, aconselha os estudantes a fazerem muitos exercícios de cálculo. “Esse tipo de conteúdo exige prática e boa interpretação”, afirma.

• Resolução de equações elementares (1º grau e 2º grau)

Em geral, os exercícios pedem para interpretar um problema em linguagem matemática e resolvê-lo. Para Nelio, do CPV, muitos vestibulandos "morrem na praia", pois erram a resolução da equação.

“O estudante deve interpretar o que está ocorrendo. Se ele vai chamar algo de ‘x’, deve saber exatamente o porquê daquela incógnita e o que ele está procurando”, diz Rodolfo.

• Triângulos: semelhança, teorema de Pitágoras

Nas questões que envolvem semelhança de triângulos e teorema de Pitágoras, geralmente o vestibulando tem dificuldade de visualizar onde esses devem ser utilizados. Normalmente não são questões contextualizadas, cobram conteúdo teórico mais a capacidade de aplicar os conceitos.

Para o docente da Oficina, “semelhança de triângulos e teorema de Pitágoras são dois conteúdos que o aluno vai ver em suas aulas de geometria plana do começo ao fim, e também são utilizados na geometria analítica e espacial. Grande parte das teorias têm como base esses conceitos”. 

• Teorema do cosseno e teorema do seno

"O aluno tem que saber a fórmula e quando e como aplicá-la. É um assunto que vem caindo bastante, como aconteceu na Unesp [Universidade Estadual Paulista] no ano passado", lembra Rodolfo. "No último dia, se você não sabe nada e quer estudar algo que pode cair, eu sugiro esse tema. Muito provavelmente será abordado e o estudante ganhará um exercício."

• Cálculo de áreas nas principais figuras geométricas

As questões que envolvem áreas são comuns tanto para os vestibulandos de exatas, biológicas ou humanas. "O conceito de área é de uso comum e de extrema importância, o que faz com que a sua incidência seja bastante acentuada", analisa o professor Nelio.

Fazer um esquema organizado é fundamental para a resolução desse tipo de conteúdo. “O aluno não precisa ser desenhista, mas isso ajuda na hora de encontrar os elementos para calcular a área”, diz Rodolfo.

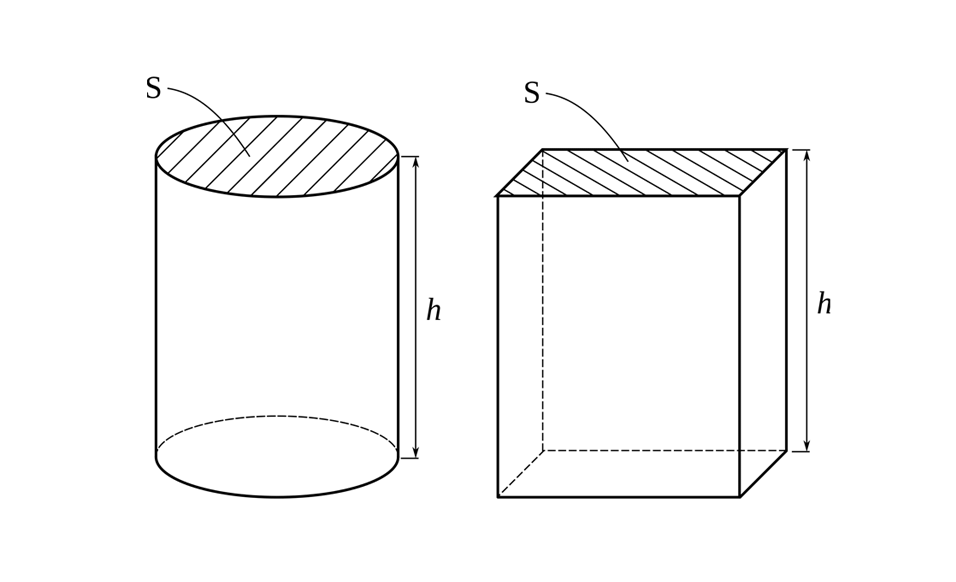
• Cálculo do volume dos principais sólidos geométricos

Já as questões de geometria podem ou não aparecer contextualizadas. Para Nelio, as questões não costumam ter alto grau de dificuldade, desde que o vestibulando não tenha restrições quanto a visualização espacial, ou seja, em 3 dimensões.

• Aplicações de logaritmos e exponenciais

As questões contextualizadas de logaritmos e exponenciais seguem o mesmo padrão, bastando que o vestibulando faça alguns modelos para poder repeti-los durante a prova. Já as questões mais teóricas cobram o domínio das propriedades dos logaritmos, calcanhar de Aquiles de muitos vestibulandos, segundo o professor Nelio, do CPV.

• Funções trigonométricas

Normalmente aparecem em questões contextualizadas que envolvem sazonalidade de oferta ou procura. “Matéria pesada e que o aluno tem dificuldade. Ele deve entender bem o círculo trigonométrico e algumas relações. Esse é um conteúdo que a teoria tem que estar na ponta da língua”, analisa o professor da Oficina.

• Probabilidade;

Juntamente com a análise combinatória, é a parte mais difícil da prova. "O vestibulando pode se preparar estudando os modelos mais comuns de questões, mas um pequeno surto de criatividade da banca examinadora faz com que a questão seja a mais difícil da prova", brinca Nelio. 

• Polinômios e equações polinomiais

Normalmente as questões de polinômios não são contextualizadas e cobram conceitos de aplicação do dispositivo de Briot-Ruffini, teorema do Resto, relações de Girard. Às vezes há envolvimento com interpretação gráfica de funções polinomiais.